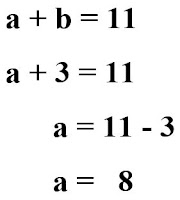Latihan soal HOTS TIU CPNS kemampuan numerik - pada kesempatan kali ini kita akan membahas salah satu aspek penilaian yang dijadikan tema soal dalam tes intelegensi umum (TIU) CPNS yaitu kemampuan numerik. Apa yang dimaksud dengan kemampuan numerik?
Kemampuan numerik adalah kemampuan melakukan operasi perhitungan dan melihat hubungan diantara angka-angka. Berdasarkan Peraturan Menteri Pendayagunaan Aparatur Negara dan Reformasi Birokrasi (Permenpanrb) Nomor 23 Tahun 2019 tentang Kriteria Penetapan Kebutuhan Pegawai Negeri Sipil dan Pelaksanaan Seleksi Calon Pegawai Negeri Sipil Tahun 2019, disebutkan terdapat empat jenis soal dalam kemampuan numerik, yaitu:
a. Berhitung adalah salah satu jenis soal dalam kemampuan numerik yang bertujuan untuk mengukur kemampuan peserta dalam melakukan perhitungan sederhana;
b. Deret angka adalah salah satu jenis soal dalam kemampuan numerik yang bertujuan untuk mengukur kemampuan peserta dalam melihat pola hubungan angka-angka;
c. Perbandingan kuantitatif adalah salah satu jenis soal dalam kemampuan numerik yang bertujuan untuk mengukur kemampuan peserta dalam menarik kesimpulan berdasarkan dua data kuantitatif;
d. Soal cerita adalah salah satu jenis soal dalam kemampuan numerik yang bertujuan untuk mengukur kemampuan peserta dalam melakukan analisis kuantitatif dari informasi yang diberikan.
Berdasarkan uraian tersebut, maka dapat kita analisis soal-soal yang berhubungan dengan aspek penilaian TIU dimaksud. Adapun soal-soal yang berhubungan dengan kemampuan numerik berhitung, deret angka, perbandingan kuantitatif dan soal cerita, yaitu:
Latihan Soal TIU CPNS - Berhitung
1. Jika a+b = 11 dan a-b = 5, maka hasil dari a2 - b2 adalah….
a. 6
b. 23
c. 55
d. 96
e. 121
Pembahasan Jawaban (Cara Biasa)
Untuk menyelesaikan soal tersebut, kita bisa menggunakan metode eliminasi dan substitusi.
Metode eliminasi
Dengan menggunakan metode eliminasi, kita bisa menghilangkan salah satu variabel agar nilai variabel lainnya dapat diketahui. Pada soal tersebut, kita akan menghilangkan variabel a untuk bisa mencari nilai variabel b.
Untuk menggunakan metode eliminasi, langkah pertama yang harus kita lakukan adalah menyamakan nilai variabel yang akan kita hilangkan. Adapun dalam soal tersebut, nilai variabel a sudah sama, sehingga kita bisa melewati langkah pertama.
Langkah kedua, tentukan tanda operasi hitung untuk menghilangkan nilai variabel a. Tanda operasi hitung yang tepat untuk menghilangkan nilai variabel a yaitu tanda kurang/minus (karena a dikurangi a sama dengan 0 atau hilang).
Langkah ketiga, lanjutkan operasi hitung tersebut sehingga hasilnya adalah 2b = 6. Kemudian, untuk mencari b kita pindah ruaskan angka 2, sehingga b = 6 dibagi 2 hasilnya yaitu b = 3. Jadi nilai variabel b adalah 3.
Metode Substitusi
Untuk mencari nilai variabel yang satunya lagi secara cepat, kita bisa menggunakan metode subsitutsi. Metode substitusi adalah suatu metode yang memanfaatkan nilai variabel yang telah diketahui untuk mencari nilai variabel yang belum diketahui. Pada soal tersebut, variabel b sudah diketahui nilainya yaitu 3, sehingga
Untuk menggunakan metode substitusi, langkah pertama yang kita lakukan adalah memilih persamaan yang sederhana sehingga mudah untuk digunakan subsitutsi. Pada soal tersebut, kedua persamaannya mudah untuk digunakan, maka kita akan pilih salah satu misal persamaan pertama yaitu a+b=11.
Langkah kedua, subsitutsi/ganti variabel b dengan nilai yang sudah diketahui yaitu 3. Langkah ketiga, pindah ruaskan angka 3 sehingga nilai a menjadi 11-3 yaitu 8.
Setelah kita mengetahui nilai variabel a dan nilai variabel b, maka kita bisa mengerjakan soal tersebut yaitu
a2 - b2 = 82 - 32
64 - 9 = 55
Jawaban c
Pembahasan Jawaban (Cara Cepat)
Apabila kita telah terbiasa melihat bentuk persamaan kuadrat, maka kita akan mengetahui bahwa
a2 - b2 hasilnya sama dengan (a + b) (a - b).
Pada soal tersebut a + b = 11 dan a - b = 5, maka hasil dari a2 - b2 = 11 x 5 = 55.
Jawaban c
Keterangan
Pertama, kita bagi pembilang angka pengali pada variabel x dan variabel y dengan 5, sehingga pembilang angka pengali pada variabel x menjadi 5 (25:5) dan variabel y menjadi 9 (45:5).
Kedua, kita bagi angka pokok variabel y dengan penyebut angka pengali variabel y, sehingga angka pokok variabel y menjadi 11 (22:2).
Setelah disederhanakan, maka kita dengan mudah mengetahui nilai dari variabel x dan variabel y
x = 5.20 = 100
y = 9.11 = 99
Berdasarkan nilai variabel x dan y tersebut, maka hubungannya adalah x > y.
Jawaban c
Latihan Soal TIU CPNS - Soal Cerita
4. Dalam suatu kelas terdapat 28 orang siswa. Apabila 15 orang siswa mengikuti ekstrakurikuler pramuka, 12 orang mengikuti ekstrakurikuler pencak silat, dan 7 orang mengikuti keduanya. Berapa orang siswa yang tidak mengikuti ekstrakurikuler pramuka dan pencak silat?
a. 8 orang
b. 9 orang
c. 10 orang
d. 11 orang
e. 12 orang
Pembahasan Jawaban
Pembahasan Jawaban (Cara Cepat)
Apabila kita telah terbiasa melihat bentuk persamaan kuadrat, maka kita akan mengetahui bahwa
a2 - b2 hasilnya sama dengan (a + b) (a - b).
Pada soal tersebut a + b = 11 dan a - b = 5, maka hasil dari a2 - b2 = 11 x 5 = 55.
Jawaban c
Latihan Soal TIU CPNS - Deret Angka
2. Perhatikan deret angka berikut ini!
3, 5, 8, 12, 17, …, …
Berapakah angka yang tepat untuk mengisi titik-titik tersebut?
a. 21, 24
b. 23, 30
c. 31, 42
d. 32, 40
e. 35, 41
Pembahasan Jawaban
2. Perhatikan deret angka berikut ini!
3, 5, 8, 12, 17, …, …
Berapakah angka yang tepat untuk mengisi titik-titik tersebut?
a. 21, 24
b. 23, 30
c. 31, 42
d. 32, 40
e. 35, 41
Pembahasan Jawaban
Kunci untuk menyelesaikan deret angka adalah menemukan pola yang konsisten. Pada soal tersebut, kita bisa melihat bahwa nilai dari kiri ke kanan terus bertambah mulai dari +2, +3, +4, +5, +6, +7.
Apabila kita sering mengerjakan soal deret angka, sebenarnya kita tidak perlu mencari sub pola karena insting kita sudah terlatih dan akan secara otomatis menemukan lanjutan pola-pola deret angka tersebut. Apalagi dalam tes CPNS waktu yang diberikan untuk mengerjakan soal sangat singkat.
Adapun sebagai bahan pembelajaran, bahwa kunci dari deret angka adalah menemukan pola yang konsisten, maka pola pada deret angka tersebut dapat dijelaskan secara rinci dengan sub pola yang kenaikan angkanya konsisten (tetap/tidak berubah) yaitu +1.
Latihan Soal TIU CPNS - Perbandingan Kuantitatif
3. Jika nilai x adalah ¼ dari 20 dan y adalah 22 ½ % dari 22, maka hubungan x dan y adalah….
a. x = 2y
b. x = y
c. x > y
d. x < y
e. x = ½ y
Pembahasan Jawaban
Untuk mempermudah penyelesaian soal, maka kita akan menyamakan terlebih dahulu bentuk variabel x dan variabel y. Bila kita lihat, angka pengali variabel y berbentuk persen maka kita ubah juga angka pengali variabel x kedalam bentuk persen. Nilai ¼ bila kita persenkan sama dengan 25%.
Ketika angka pengali variabel x dan variabel y sudah sama bentuknya yaitu persen, maka kita sama-sama hilangkan persen tersebut, sehingga angka pengali variabel x dari 25% menjadi 25 dan angka pengali variabel y dari 22 ½ % menjadi 22 ½.
Kemudian, untuk mempermudah perhitungan maka angka pengali variabel y kita ubah dari pecahan campuran menjadi pecahan biasa. Angka 22 ½ bila kita ubah menjadi pecahan biasa menjadi 45/2.
Selanjutnya, kita akan mempermudah perhitungan dengan cara menyederhanakannya:
Pertama, kita bagi pembilang angka pengali pada variabel x dan variabel y dengan 5, sehingga pembilang angka pengali pada variabel x menjadi 5 (25:5) dan variabel y menjadi 9 (45:5).
Kedua, kita bagi angka pokok variabel y dengan penyebut angka pengali variabel y, sehingga angka pokok variabel y menjadi 11 (22:2).
Setelah disederhanakan, maka kita dengan mudah mengetahui nilai dari variabel x dan variabel y
x = 5.20 = 100
y = 9.11 = 99
Berdasarkan nilai variabel x dan y tersebut, maka hubungannya adalah x > y.
Jawaban c
Latihan Soal TIU CPNS - Soal Cerita
4. Dalam suatu kelas terdapat 28 orang siswa. Apabila 15 orang siswa mengikuti ekstrakurikuler pramuka, 12 orang mengikuti ekstrakurikuler pencak silat, dan 7 orang mengikuti keduanya. Berapa orang siswa yang tidak mengikuti ekstrakurikuler pramuka dan pencak silat?
a. 8 orang
b. 9 orang
c. 10 orang
d. 11 orang
e. 12 orang
Pembahasan Jawaban
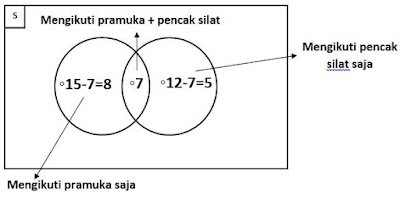
Untuk menyelesaikan soal tersebut, kita bisa menggunakan diagram venn.
Langkah pertama, kita buat sebuah persegi panjang berukuran besar ditambah dengan sebuah persegi berukuran kecil di ujung kiri atas dengan simbol huruf “S” di dalam persegi kecil tersebut.
Huruf “S” merupakan kependekan dari semesta yang artinya keseluruhan. Artinya, seluruh himpunan yang diungkapkan dalam soal, terkandung dalam diagram venn yang dibuat.
Langkah kedua, kita cari tahu apakah dalam himpunan tersebut terdapat irisan atau tidak? Bila kita analisis, pada soal tersebut terdapat irisan antara himpunan siswa yang mengikuti pramuka dengan himpunan siswa yang mengikuti pencak silat yaitu sebanyak 7 orang, sehingga untuk merepresentasikannya kita harus menggambar dua buah lingkaran yang saling beririsan dan ditengah irisan tersebut kita masukan angka 7. Alasannya, karena terdapat 7 orang yang mengikuti pramuka dan pencak silat sekaligus.
Langkah ketiga, kita hitung jumlah siswa yang mengikuti pramuka saja. Pada soal, telah disebutkan terdapat 15 orang siswa yang mengikuti pramuka dan ada 7 orang yang mengikuti pramuka dan pencaksilat, sehingga untuk menentukan jumlah siswa yang mengikuti pramuka saja yaitu 15 - 7 = 8 orang siswa.
Adapun untuk menentukan jumlah siswa yang mengikuti pencak silat saja, yaitu 12 - 7 = 5 orang siswa.
Langkah keempat, tinggal kita hitung jumlah siswa yang tidak mengikuti pramuka dan pencak silat, yaitu 28 - 8 - 7 - 5 = 8 orang siswa.
Jawaban a
Demikian latihan soal HOTS TIU CPNS mengenai kemampuan numerik berhitung, deret angka, perbandingan kuantitatif, dan soal cerita berdasarkan Permenpanrb Nomor 23 Tahun 2019, semoga bermanfaat. Bila ada kekeliruan, pertanyaan dan saran mohon agar disampaikan di kolom komentar, terima kasih.
Daftar Isi - Informasi dan Latihan Soal Lengkap Tes CPNS Terbaru
Daftar Isi - Informasi dan Latihan Soal Lengkap Tes P3K Terbaru
Channel Telegram Seleksi P3K dan CPNS Terbaru
